Algorithm：CNN原理解读

前言

卷积神经网络（Convolutional Neural Network，CNN）是一种在计算机视觉领域取得了巨大成功的深度学习模型。它们的设计灵感来自于生物学中的视觉系统，旨在模拟人类视觉处理的方式。在过去的几年中，CNN已经在图像识别、目标检测、图像生成和许多其他领域取得了显著的进展，成为了计算机视觉和深度学习研究的重要组成部分
在人工智能的浪潮中，卷积神经网络(CNN)以其卓越的性能在图像识别、视频处理等领域大放异彩。它通过模拟人脑视觉系统，利用卷积层、池化层等结构，从数据中自动提取并学习特征，实现高效且准确的分类与识别。

定义

卷积神经网络(Convolutional Neural Networks, CNN)是一类包含卷积计算且具有深度结构的前馈神经网络(Feedforward Neural Networks)。它通过卷积操作来提取输入数据的局部特征，并通过多层卷积和池化操作形成复杂的特征表示，最终通过全连接层进行分类或回归等任务。
CNNIntroduce1

特点

1.局部连接: 卷积层中的神经元仅与输入数据的一个局部区域(即局部感受野)相连，这有助于捕捉图像的局部特征。
CNNIntroduce2
2.权值共享: 同一个卷积核在输入数据的所有位置上共享权重，这大大减少了网络的参数数量，降低了模型的复杂度。
3.平移不变性: 无论输入数据中的特征出现在哪个位置，卷积操作都能提取到相同的特征，这使得卷积神经网络在处理图像等具有网络结构的数据时具有很高的效率和准确性。
CNNIntroduce3

基本结构

卷积神经网络的基本结构通常由以下几个部分组成：
输入层(Input Layer): 接收原始图像数据或其他类型的网格结构数据。
卷积层(Convolution Layer): 通过卷积操作提取输入数据的局部特征。卷积层中的每个卷积核可以提取一种特定的特征，多个卷积核可以并行工作以提取不同类型的特征。
池化层(Pooling Layer): 对卷积层的输出进行下采样(或称为降维)，以减少参数数量和提高计算效率。常见的池化操作包括最大池化和平均池化。
全连接层(Fully Connected Layer): 将前面层提取的特征综合起来，用于分类或回归等任务。全连接层的每个神经元都与前一层的所有神经元相连。
CNNIntroduce4

输入层(Input Layer)

在神经网络中，输入层(Input Layer)是神经网络的第一层，负责接收外部输入的数据。这些数据可以说图像、声音、文本、传感器数据等。输入层的主要作用是将这些数据以数值的形式传递给网络，以便于进行后续的处理和分析。
假设我们正在设计一个用于手写数字识别的神经网络(如MNIST数据集)，该数据集包含0到9的手写数字图像，每张图像的大小为28×28像素。这这种情况下，输入层包含784个神经元(因为28×28=784)，每个神经元对应图像中的一个像素。这些像素值(通常是灰度值，范围从0到255)在输入到网络之间可能会进行归一化处理，即将他们缩放到0到1之间。
CNNIntroduce5
图像在计算机中是一对按顺序排列的数字，数值为0到255。0表示最高，255最亮。

卷积层(Convolution Layer)

卷积层(Convolution Layer)是卷积神经网络(Convolutional Neural Network,CNN)中的核心层(核心组件)之一，它主要负责在输入图像上执行卷积操作，以提取输入图像中的不同特征。卷积层通过卷积核(滤波器或特征检测器)与输入图像进行局部连接和卷积运算，以生产特征图(Feature Map),这些特征图包含了输入数据的不同特征信息。
CNNIntroduce6

Input表示输入的特征图，数字为像素点的值，其中黄色的部分表示卷积核的关注区域。kernel表示了一个尺寸为3×3的卷积核，其中绿色部分表示卷积核的权重。output表示经过卷积运算后得到的输出结果，其黄色区域标识的就是卷积的运算结构。

$$ Output = 2\times (-1)+1\times0+0\times1+9\times(-1)+5\times0+ \ 4\times1+2\times(-1)+3\times0+4\times1=-5 $$

CNNIntroduce7

参数详解:
卷积核大小(Kernel Size): 定义了卷积操作时覆盖的输入数据区域大小，影响特征提取的尺度。
步长(Stride): 卷积核在输入数据上滑动的距离，影响输出特征图的尺寸。
填充(Padding): 在输入数据边缘添加的额外像素，用于控制输出特征图的尺寸。
输入/输出通道数(In/Out Channels): 输入数据的深度/通道数和输出特征图的数量，决定了卷积层处理的深度和能够生成的特征图种类。

池化层(Pooling Layer)

池化层(Pooling Layer)是深度学习神经网络中常用的一种层级结构，主要用于减小输入数据的空间尺寸，降低模型的计算复杂度，减少过拟合，并在一定程度上提取输入数据的重要特征。池化层主要对卷积层输出的特征图进行下采样操作，一般跟在卷积层之后。
CNNIntroduce8

主要功能:
特征降维(下采样): 通过减小特征图的尺寸来降低计算量，并且可以提取出特征图的主要信息;
特征不变性: 池化操作使模型更加关注是否某些特征是否存在，而不是特征具体的位置，特征不变性包括平移不变性、旋转不变性和尺度不变形。
防止过拟合: 通过减小数据量和参数个数，降低模型的复杂度，提高模型的泛化能力。

全连接层(Fully Connected Layer)

全连接层(Fully Connected Layer)是深度学习常用的一种神经网络层，常用于图像识别等，它的主要作用是学习到前面层(如卷积层、池化层等)输出的特征，进行全局整合，并映射到样本的标记空间(输出空间)。
CNNIntroduce9

在全连接层中，每个神经元都与前一层的所有神经元相连，以实现全局特征的加权组合。通过对特征权重和偏置的学习，使得神经网络能够提取到更有意义的特征。全连接层通过其全连接的特性，能够整合输入数据的全局特征，并将这些特征进一步映射到输出层，以实现最终的分类或回归任务。

应用领域

卷积神经网络在计算机视觉、自然语言处理、语音识别等领域有着广泛的应用。以下是一些具体的应用示例:
1.计算机视觉: 图像分类(如识别猫、狗、车等物体)、目标检测(如检测车辆、行人、交通标志等)、图像分割(如医学影像中的器官分割)、人脸识别、图像搜索等。
2.自然语言处理: 情感分析、文本分类、命名实体识别等。
3.语音识别: 识别语音指令、语音转文本等。
4.视频分析: 动作识别、视频内容理解等。

Q&A

计算机在输入层对图像的处理方式

对于计算机图像就是一堆按顺序排列的数字，其中黑白图像和彩色图像规则各不相同：
1.黑白图像
计算机使用0到255来表明每个像素的暗度，0表示最暗，255表示最亮，如下图:
CNNIntroduce5
2.彩色图片
彩色图片一般使用RGB颜色模型(也分别对应着R、G、B三个通道)，即红、绿、蓝三原色的色光以不同的比例相加，来产生多种多样的色光。RGB颜色模型中，单个矩阵就扩展成了有序排列的三个矩阵，也可以用三维的张量去理解。其中的每一个矩阵又叫这个图片的一个channel(通道)，用宽、高、深来描述。
CNNIntroduce10
CNNIntroduce16

卷积神经网络与传统神经网络的对比

在传统神经网络中，我们要识别下图红色框中的图像时，我们很可能识别不出来，因为这六张图的位置都不通，计算机无法分辨出他们其实是一种形状或物体。
CNNIntroduce11
传统的神经网络如下图:
CNNIntroduce12
我们希望一个物体不管在画面左侧还是右侧，都会被识别为同一物体，这一特点就是不变性。为了实现平移不变性，卷积神经网络（CNN）等深度学习模型在卷积层中使用了卷积操作，这个操作可以捕捉到图像中的局部特征而不受其位置的影响。
CNNIntroduce13

在卷积神经网络中，卷积操作是指将一个可移动的小窗口（称为数据窗口，如下图绿色矩形）与图像进行逐元素相乘然后相加的操作。这个小窗口其实是一组固定的权重，它可以被看作是一个特定的滤波器（filter）或卷积核。这个操作的名称“卷积”，源自于这种元素级相乘和求和的过程。这一操作是卷积神经网络名字的来源。
简而言之，卷积操作就是用一个可移动的小窗口来提取图像中的特征，这个小窗口包含了一组特定的权重，通过与图像的不同位置进行卷积操作，网络能够学习并捕捉到不同特征的信息。

为什么要进行数据填充?

需要注意的参数

a.步长stride: 每次滑动的位置步长。
b.卷积核的个数: 决定输出的depth厚度。同时代表卷积核的个数.
c.填充值zero-padding: 在外围边缘补充若干圈0，方便从初始位置以步长为单位可以刚好滑倒末尾位置，通俗地讲就是为了总长能被步数整除。

为什么要进行数据填充?zero-padding存在意义?

假设有一个大小为4×4的输入图像:

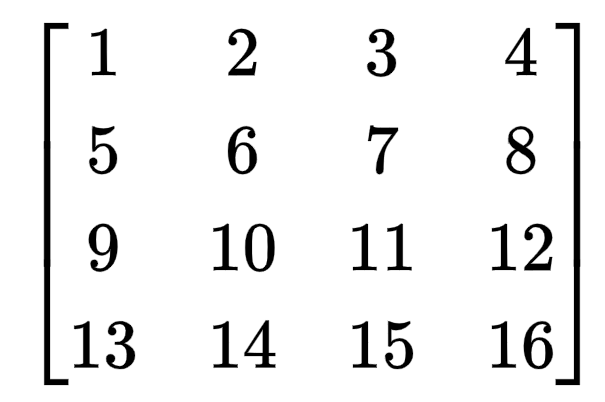
CNNIntroduce14

现在，我们要应用一个 3x3 的卷积核进行卷积操作，步幅（stride）为 1，且要使用填充（padding）为 1。如果不使用填充，卷积核的中心将无法对齐到输入图像的边缘，导致输出特征图尺寸变小。假设我们使用步幅（stride）为 1 进行卷积，那么在不使用填充的情况下，输出特征图的尺寸将是 2x2。
所以我们要在它的周围填充一圈0，填充为 1 意味着在输入图像的周围添加一圈零值。添加填充后的图像：